Atomic floating-point min/max
Document number: P3008R0.
Date: 2023-10-13.
Authors: Gonzalo Brito Gadeschi, David Sankel <dsankel@adobe.com>.
Reply to: gonzalob at nvidia.com .
Audience: SG1, LEWG.
Table of Contents
Introduction
P0493R4 Atomic minimum/maximum proposes the addition of atomic<T>::fetch_min and atomic<T>::::fetch_max operations, which atomically perform std::min and std::max computations.
The Varna '23 plenary rejected these semantics for atomic<floating-point> types due to safety concerns. These semantics deviate from the current standard practice, as defined by IEEE 754-2019 recommendations and the capabilities of available hardware.
This paper aims to empower the committee to ship these APIs in the C++ 26 timeframe. It reviews the semantics proposed in P0493R4 and standard practice: IEEE 754-2008, IEEE 754-2019, and available hardware support. It then explores the design space and evaluates alternative solutions.
Finally, the authors propose two coherent alternatives and concrete wording changes to align P0493R4 with some of the semantics IEEE 754-2019 recommends all vendors implement.
Survey of programming language floating-point min/max API semantics
This section provides an overview of widely used floating-point min/max semantics. We will focus on how various min/max semantics handle the following “corner cases”:
- Signed zero: Should
-0 be considered less than +0 (-0 < +0), or should -0 and +0 be treated as equivalent (-0 == +0) such that, e.g., min(+0, -0) = +0?
- One quiet NaN (qNaN): when one of the arguments is a qNaN, should it be treated as Missing Data and the other argument returned, or should it be treated as an Error and propagated?
- Missing Data: returns the other argument:
min(x, qNaN) = x and min(qNaN, x) = x.
- Error: propagates the qNaN:
min(x, qNaN) = qNaN and min(qNaN, x) = qNaN.
Explicitly and intentionally, this paper ignores:
- Signaling NaNs: C specifies they are undefined, and C++ does not specify anything about them.
- NaN payload propagation: IEEE 754 does not mandate it, and programming languages do not interpret NaN payloads.
Table 1 summarizes the semantics of the different C or C++ APIs regarding Signed Zeros and Quiet NaN handling and documents whether implementations that implement particular IEEE 754 semantics are valid implementations of the APIs.
| C API |
C++ API |
Signed Zeros |
One qNaN |
IEEE 754 impl valid? |
| - |
min
max |
Equivalent |
Undefined
(Second[1]) |
Ternary [0] |
fmin
fmax |
- |
Equivalent
or
-0 < +0 (QoI) [2] |
Missing Data |
minNum
maxNum
or (QoI)
minimumNumber
maximumNumber |
fminimum
fmaximum |
- |
-0 < +0 |
Error |
minimum
maximum |
fminimum_num
fmaximum_num |
- |
-0 < +0 |
Missing Data |
minimumNumber
maximumNumber |
[0] Ternary semantics: min(x,y) = y < x? y : x, max(x,y) = x < y? y : x; both return the first argument if the arguments are equivalent.
[1] In practice, the same implementation as for valid values is used, and the second argument is returned, since in the ternary expression, the conditional involving a NaN is always false.
[2] QoI: “Quality of Implementation”, i.e., fmin does not require -0 < +0, but it recommends that high quality implementations implement it.
C++ std::min/std::max
The std::min and std::max algorithms have a precondition on their arguments ([alg.min.max.1]):
Preconditions: For the first form, T meets the Cpp17LessThanComparable requirements (Table Cpp17LessThanComparable).
which NaNs do not satisfy.
Rationale.
Per [structure.requirements#4] and [structure.requirements#8], which uses floating points as an example, the syntactic requirements apply to the type, but the semantic requirements only apply to the values actually passed to the algorithm.
The Cpp17LessThanComparable concept, which requires:
< is a strict weak ordering relation ([alg.sorting])
Which is specified in [alg.sorting#general-4]:
The term strict refers to the requirement of an irreflexive relation (!comp(x, x) for all x), and the term weak to requirements that are not as strong as those for a total ordering, but stronger than those for a partial ordering. If we define equiv(a, b) as !comp(a, b) && !comp(b, a), then the requirements are that comp and equiv both be transitive relations:
comp(a, b) && comp(b, c) implies comp(a, c)equiv(a, b) && equiv(b, c) implies equiv(a, c)
[Note 1: Under these conditions, it can be shown that
3. equiv is an equivalence relation,
4. comp induces a well-defined relation on the equivalence classes determined by equiv, and
5. the induced relation is a strict total ordering.
— end note]
and is satisfied by all floating-point values with the exception of NaNs.
For valid values, implementations follow ([alg.min.max]):
[std::min]:
Returns: The smaller value. Returns the first argument when the arguments are equivalent.
[std::max]:
Returns: The larger value. Returns the first argument when the arguments are equivalent.
which preserves equivalence between -0 and +0 (godbolt):
auto min = [](auto& a, auto& b) -> auto& { return std::min(x, y); };
auto max = [](auto& a, auto& b) -> auto& { return std::max(x, y); };
min(qNaN, 2.f);
max(qNaN, 2.f);
min(2.f, qNaN);
max(2.f, qNaN);
min(-0.f, +0.f);
max(-0.f, +0.f);
min(+0.f, -0.f);
max(+0.f, -0.f);
In all standard library implementations surveyed, the manifestation of the undefined behavior is to return the first argument; this is depicted in the example with “UB: qNaN” and “UB: 2”.
The behavior of these semantics are:
- Signed Zero: equivalent.
- One qNaN: undefined.
In concurrent programs, these semantics become even less i
C fmin/fmax
The semantics of the ISO/IEC 9899:2024 (C23) standard fmin/fmax functions are compatible with implementations of IEEE 754-2008 minNum and maxNum and of IEEE 754-2019 minimumNumber/maximumNumber. The fmin/fmax functions are available in C++ through the <cmath> header as std::fmin/std::fmax.
The semantics of C’s fmin/fmax
- Signed zero:
-0 may be equivalent to +0 (minNum/maxNum)-0 < +0 allowed as QoI (minimumNumber/maximumNumber guarantee it).
- One qNaN: missing data (other value returned).
(collapsible) C23 fmin/fmax specification.
[From C23 7.12.12 Maximum, minimum, and positive difference functions]
[fmax 7.12.12.2]: The fmax functions determine the maximum numeric value of their arguments. [Note 299]
[fmin 7.12.12.3]: The fmin functions determine the minimum numeric value of their arguments. [Note 300]
[Note 299]: Quiet NaN arguments are treated as missing data: if one argument is a quiet NaN and the other numeric, then the fmax functions choose the numeric value. See F.10.9.2.
[Note 300]: The fmin functions are analogous to the fmax functions in their treatment of quiet NaNs.
[Note 461]: Ideally, fmax would be sensitive to the sign of zero, for example fmax(−0.0, +0.0) would return +0; however, implementation in software might be impractical.
NOTE 1: The fmax and fmin functions are similar to the fmaximum_num and fminimum_num functions, though may differ in which signed zero is returned when the arguments are differently signed zeros and in their treatment of signaling NaNs (see F.10.9.5).
[F.10.9.2 The fmax functions]: If just one argument is a NaN, the fmax functions return the other argument (if both arguments are NaNs, the functions return a NaN).
[F.10.9.3 The fmin functions]: The fmin functions are analogous to the fmax functions (see F.10.9.2).
[F.2.1]: This specification does not define the behavior of signaling NaNs.
(collapsible) [IEEE 754-2008] minNum/maxNum specification.
[5.3.1 General operations]
sourceFormat minNum(source, source)
sourceFormat maxNum(source, source)
minNum(x, y) is the canonicalized number x if x<y, y if y<x, the canonicalized number if one operand is a number and the other a quiet NaN. Otherwise it is either x or y, canonicalized (this means results might differ among implementations).
maxNum(x, y) is the canonicalized number y if x<y, x if y<x, the canonicalized number if one operand is a number and the other a quiet NaN. Otherwise it is either x or y, canonicalized (this means results might differ among implementations).
That is, in the presence of a qNaN, these return the value, but signed zeros may or may not be equivalent:
fmin(qNaN, 2.f): 2
fmax(qNaN, 2.f): 2
fmin(2.f, qNaN): 2
fmax(2.f, qNaN): 2
fmin(-0.f, +0.f): -0 or +0
fmax(-0.f, +0.f): -0 or +0
fmin(+0.f, -0.f): -0 or +0
fmax(+0.f, -0.f): -0 or +0
IEEE 754-2019 removed minNum andmaxNum operations and replaced them with minimumNumber/maximumNumber and minimum/maximum. These are surveyed in the next section. The gist of the rationale for their removal from The Removal/Demotion of MinNum and MaxNum Operations from IEEE 754-2018 is:
These [minNum, maxNum] operations are removed from or demoted in IEEE std 754-2018, due to their non-associativity. […] With this non-associativity, different compilations or runs on parallel processing can return different answers […].
C23 minimum/maximum/minimumNumber/maximumNumber
IEEE 754-2019 removed minNum/maxNum and recommends programming languages to provide their replacements instead: minimumNumber/maximumNumber/minimum/maximum.
(collapsible) IEEE 754-2019 minimum/maximum/minimumNumber/maximumNumber specification.
[9.6 Minimum and maximum operations]: Language standards should define the following homogeneous general-computational operations for all
supported arithmetic formats:
sourceFormat minimum(source, source)
sourceFormat minimumNumber(source, source)
sourceFormat maximum(source, source)
sourceFormat maximumNumber(source, source)
minimum(x, y) is x if x < y, y if y < x, and a quiet NaN if either operand is a NaN, according to 6.2. For this operation, −0 compares less than +0. Otherwise (i.e., when x=y and signs are the same) it is either x or y.
minimumNumber(x, y) is x if x<y, y if y<x, and the number if one operand is a number and the other is a NaN. For this operation, −0 compares less than +0. If x = y and signs are the same it is either x or y. If both operands are NaNs, a quiet NaN is returned, according to 6.2.
maximum(x, y) is x if x > y, y if y > x, and a quiet NaN if either operand is a NaN, according to 6.2. For this operation, +0 compares greater than −0. Otherwise (i.e., when x=y and signs are the same) it is either x or y.
maximumNumber(x, y) is x if x>y, y if y>x, and the number if one operand is a number and the other is a NaN. For this operation, +0 compares greater than −0. If x = y and signs are the same it is either x or y. If both operands are NaNs, a quiet NaN is returned, according to 6.2.
[6.2 Operations with NaNs]: For an operation with quiet NaN inputs, except as stated otherwise, if a floating-point result is to be delivered the result shall be a canonical quiet NaN.
(collapsible) C23 fmaximum/fminimum/fmaximum_num/fminimum_num specification.
[From C23 7.12.12 Maximum, minimum, and positive difference functions]
[fmaximum - 7.12.12.4]: The fmaximum functions return the maximum value of their arguments.
The fmaximum functions determine the maximum value of their arguments. For these functions, +0 is considered greater than −0. These functions differ from the fmaximum_num functions only in their treatment of NaN arguments (see F.10.9.4, F.10.9.5).
[fminimum - 7.12.12.5]: The fminimum functions return the minimum value of their arguments.
The fminimum functions determine the minimum value of their arguments. For these functions, −0 is considered less than +0. These functions differ from the fminimum_num functions only in their treatment of NaN arguments (see F.10.9.4, F.10.9.5).
[fmaximum_num - 7.12.12.8]: The fmaximum_num functions return the maximum value of their numeric arguments.
The fmaximum_num functions determine the maximum value of their numeric arguments. They determine the number if one argument is a number and the other is a NaN. These functions differ from the fmaximum functions only in their treatment of NaN arguments (see F.10.9.4, F.10.9.5).
[fminimum_num - 7.12.12.9]: The fminimum_num functions return the minimum value of their numeric arguments.
The fminimum_num functions determine the minimum value of their numeric arguments. They determine the number if one argument is a number and the other is a NaN. These functions differ from the fminimum functions only in their treatment of NaN arguments (see F.10.9.4, F.10.9.5).
[F.10.9.4]: These functions treat NaNs like other functions in <math.h> (see F.10).
[F.10 Mathematics <math.h> and <tgmath.h>]: Functions with a NaN argument return a NaN result and raise no floating-point exception, except
where explicitly stated otherwise.
The semantics of these functions matches for signed zero: -0 < +0, and differs in their treatment when one argument is a qNaN:
- Missing Data:
fminimumNumber/fmaximumNumber, return the Number.
- Errors:
fminimum/fmaximum, propagate the qNaN.
fminimum(qNaN, 2.f): qNaN
fmaximum(qNaN, 2.f): qNaN
fminimum(2.f, qNaN): qNaN
fmaximum(2.f, qNaN): qNaN
fminimum(-0.f, +0.f): -0
fmaximum(-0.f, +0.f): +0
fminimum(+0.f, -0.f): -0
fmaximum(+0.f, -0.f): +0
fminimum_num(qNaN, 2.f): 2
fmaximum_num(qNaN, 2.f): 2
fminimum_num(2.f, qNaN): 2
fmaximum_num(2.f, qNaN): 2
fminimum_num(-0.f, +0.f): -0
fmaximum_num(-0.f, +0.f): +0
fminimum_num(+0.f, -0.f): -0
fmaximum_num(+0.f, -0.f): +0
Impact of replacing min with fminimum_num
Table 2 captures the impact of replacing min with fminimum_num is as follows:
std::min/std::max |
fminimum_num/fmaximum_num |
min(qNaN, 2.f); // UB: qNaN
max(qNaN, 2.f); // UB: qNaN
min(+0.f, -0.f); // +0
max(-0.f, +0.f); // -0 |
fminimum_num(qNaN, 2.f); // 2
fmaximum_num(qNaN, 2.f); // 2
fminimum_num(+0.f, -0.f); // -0
fmaximum_num(-0.f, +0.f); // +0 |
That is, when the first input of std::min/std::max is a qNaN, then these switch from exhibiting undefined behavior to returning a number, and when signed zeros are involved, there is a case where the result has a different sign.
Survey of hardware atomic floating-point min/max API semantics
On systems without native support for atomic floating-point min/max operations, these operations must be performed atomically, e.g., using a CAS loop, a compare-and-conditional-store loop, an LL/SC loop, or, e.g., by taking a lock, which would make the atomic not lock-free. In these systems, the memory latency overhead may outweight the cost of performing the actual arithmetic portion of the min/max operations, and extra effort may be required to ensure forward progress properties like starvation freedom, and therefore those systems are not considered here.
Table 3 surveys the publicly known Instruction Set Architectures (ISAs) with atomic floating-point min/max operations, which are all GPU ISAs:
| Vendor |
ISA |
Instructions |
IEEE-2019 compat |
Signed Zero |
Quiet NaN |
| AMD |
CDNA2+ |
MIN
MAX |
minimumNumber
maximumNumber |
-0 < +0 |
Missing Data |
| Intel |
Xe ISA |
AOP_FMIN
AOP_FMAX [0] |
minimumNumber
maximumNumber |
-0 < +0 |
Missing Data |
| NVIDIA |
PTX |
atom
red |
minimumNumber
maximumNumber |
-0 < +0 |
Missing Data |
| Neutral [1] |
SPIR-V Extension |
OpAtomicFMinEXT
OpAtomicFMaxEXT |
C fmin/fmax |
Equivalent;
QoI: -0 < +0 |
Missing Data |
- [0]: Volume 2d: Command Reference: Structures, page 229.
- [1]: The Vulkan extension corresponding to this SPIR-V extension is
VK_EXT_shader_atomic_float2. Hardware that implements it is listed here and here.
All the architectures surveyed order -0 < +0, treat qNaNs as missing data, and implement IEEE 754-2019 minimumNumber and maximumNumber semantics. The SPIR-V extension requires C fmin/fmax semantics, which allows -0 < +0 but does not require it.
The semantics vendor implement are compatible with C23’s fminimum_num/fmaximum_num, and C’s fmin/fmax, but not with C++'s std::min/std::max due to the different outcomes when signed-zeros are involved.
We compare the performance impact of two different atomic<floating-point>::fetch_max semantics:
std::min, which lowers to a CAS-loop that performs std::min (similar for compare-and-conditional-store), andfminimum_num, which lowers to native atomic operations,
using a synthetic micro-benchmark that measures throughput in Giga Operations per Second (y-axis; logarithmic) as a function of the number of threads (x-axis; logarithmic) from 32 to 130’000 hardware threads on an .
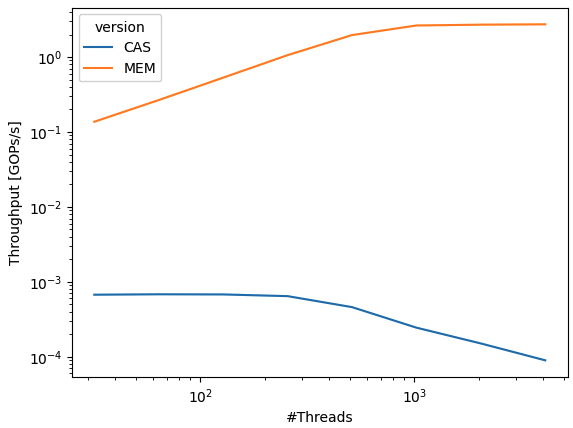
Modern concurrent systems provide dozens of millions of hardware threads operating on the same shared memory.
While native in-memory atomic operations increase throughput until its theoretical peak with just a few thousand threads, the performance of compare and swap strategies decreases as the number of threads increases due to excess contention. At just a few thousand threads, the performance is already four orders of magnitude worse (~10’000x) than that of native in-memory operations. This is why vendors of highly concurrent systems provide these operations.
While most CPU ISAs lack native hardware instructions for atomic floating-point min/max, their performance impact is expected to be similar to that of atomic integer min/max. Section 9 of P0493R4 presents benchmarks comparing the performance of a CAS-based implementation against an Arm v8.1 implementation using the native atomic ldsmaxl instruction. The benchmark covers a range of cores, from 2 to 64. The performance improvement of the native instruction ranges between 2.75x (2 cores) to 1.7x at 64 cores. We expect this behavior to transfer to atomic floating-point min/max.
We, unfortunately, do not have benchmarks for other hardware configurations at this time.
Design space
The design space can be categoratized into two groups of alternatives:
- Same semantics:
::fetch_min/_max have same semantics as std::min/std::max,
- Different semantics:
::fetch_min/_max have different semantics than std::min/std::max.
The following table shows the subjectively most reasonable alternative of each category side-by-side, along with a summary of their advantages and disadvantages, which are analyzed in the following section.
Table 4: Comparison of best alternative of each category.
| Category |
std::min semantics |
std::fminimum_num semantics |
| Concrete Example |
x.fetch_min(y);
x.fetch_fminimum_num(y); |
x.fetch_min(y, std::less{});
x.fetch_min(y); |
| Pros |
- Parallelizing preserves semantics:
NaNs are UB & -0 == +0.
- Consistency in standard. |
- Safer semantics by default.
- Hardware acceleration by default.
|
| Cons |
- The convenient name, min, has unportable behavior.
- The convenient name has degraded performance.
|
|
| Training reqs. |
Misuse and Performance. |
Subtle surprising behavior change for floating-point. |
| Default |
Stability. |
Correctness + Performance. |
| Opt-in |
Correctness + Performance. |
Stability. |
.
Alternatives that reserve fetch_min/fetch_max for std::min/std::max
In this group of alternatives, exposure of different semantics shall happen through other APIs, and we may potentially expose one or more of the following:
fetch_min/fetch_max with std::min/std::max semantics, orfetch_fminimum/fetch_fmaximum with fminimum/fmaximum semantics, orfetch_fminimum_num/fetch_fmaximum_num with fminimum_num/fmaximum_num semantics, orfetch_min/fetch_max API accepting a defaulted comparison function object Cmp that satisfies the requirements of Compare and defaults to std::less, potentially providing other function objects to choose minimum/minimumNumber semantics.
template <floating-point> struct less_fminimum;
template <floating-point> struct less_fminimum_num;
template <floating-point> struct less_fmaximum;
template <floating-point> struct less_fmaximum_num;
template <floating-point>
class atomic {
using T = floating-point;
T fetch_min(T x, memory_order = memory_order_seq_cst);
T fetch_max(T x, memory_order = memory_order_seq_cst);
T fetch_fminimum(T x, memory_order = memory_order_seq_cst);
T fetch_fmaximum(T x, memory_order = memory_order_seq_cst);
T fetch_fminimum_num(T x, memory_order = memory_order_seq_cst);
T fetch_fmaximum_num(T x, memory_order = memory_order_seq_cst);
template <typename Compare>
T fetch_max(T other, Compare cmp = std::less, memory_order ord = memory_order_seq_cst);
template <typename Compare>
T fetch_min(T other, Compare cmp = std::less, memory_order ord = memory_order_seq_cst);
};
x.fetch_min(y);
x.fetch_min(y, less_fminimum{});
The advantage of these alternatives is that they preserve the semantics of sequential code that uses std::min when it is made concurrent via fetch_min.
The disadvantages of these alternatives are that the fetch_min/_max semantics are unintuitive for floating-point numbers and error prone, and do not benefit from any hardware acceleration available as surveyed in Table 2.
Generic programmers willing to avoid these disadvantages need to opt-in to wrapping these APIs as follows:
template <typename T>
T atomic_min_wrapper(atomic<T>& x, T& y) {
if constexpr(std::is_floating_point_v<T>) {
return x.fetch_fminimum(y);
}
return x.fetch_min(y);
}
But creating such wrappers requires developers to be aware of essentially everything discussed in this proposal until this point.
Such awareness may be enforced by not providing fetch_min/fetch_max APIs for floating-point atomics at all, and instead only provide the fetch_fminimum and related APIs, requiring developers to explicitly pick the semantics, and making wrappers like the one in Listing 5 mandatory for writing generic code.
Alternatives that provide fetch_min/fetch_max with different semantics
There is precendent in the C++ standard for the atomic operations semantics to deviate from the non-atomic semantics. For example, atomic<int>::fetch_add wraps around on overflow, instead of exhibiting undefined behavior, see [atomics#ref.int-6]:
Remarks: For signed integer types, the result is as if the object value and parameters were converted to their corresponding unsigned types, the computation performed on those types, and the result converted back to the signed type.
[Note 2: There are no undefined results arising from the computation. — end note]
In a similar spirit, atomic<floating-point>::fetch_min/::fetch_max operations could be specified to be well-defined for NaNs and to respect -0 < +0.
If we restricts the specification to the semantics available in the scalar floating-point functions, we have 3 different options:
fminimum/fmaximum: NaNs are propagated as errors and -0 < +0.- NaNs are treated as missing data, i.e., the number is returned when one argument is a NaN, and
fminimum_num/fmaximum_num: -0 < +0.fmin/fmax: -0 == +0 or (QoI) -0 < +0.
The semantics chosen could be complemented with a fetch_min/fetch_max API that accepts a comparison object that needs to satisfy the requirements of Compare but also allows accepting, e.g., one of a set of floating-point-specific blessed comparison-like objects provided by the standard that handle NaNs in specific ways but do not provide a strict weak ordering when NaNs are present. This enables applications to pick whether, e.g., they want to treat NaNs as missing data, or as errors, or whether they want to treat -0 as equivalent to +0, or as +0 greater than -0.
For example, C++ could do some or all of:
template <floating-point> struct less_fminimum;
template <floating-point> struct less_fminimum_num;
template <floating-point> struct less_fmaximum;
template <floating-point> struct less_fmaximum_num;
template <floating-point>
class atomic {
using T = floating-point;
T fetch_min(T x, memory_order = memory_order_seq_cst);
T fetch_max(T x, memory_order = memory_order_seq_cst);
template <typename Compare>
T fetch_max(T other, Compare cmp = fminimum_num{}, memory_order ord = memory_order_seq_cst);
template <typename Compare>
T fetch_min(T other, Compare cmp = fminimum_num{}, memory_order ord = memory_order_seq_cst);
};
x.fetch_min(y);
x.fetch_min(y, less_fminimum{});
x.fetch_min(y, less_fminimum_num{});
x.fetch_min(y, less{});
These groups of alternatives give applications the capability to write generic code which may encounter floating-point values and then exhibits reasonable behavior and benefits from hardware acceleration, without requiring developers of being aware of most of what has been discussed in this paper.
If a developer encounters different results when porting their sequential code using std::min to fetch_min, discovering those differences is required to notice that the developer may want to opt-in to the std::min semantics. This feedback loop is - for better or worse - more direct than requiring the developer to be a floating-point expert. If the differences are due to NaNs, then the original sequential program already exhibited undefined behavior, but the differences may be due to the treatment of -0 == +0 in the sequential implementation, which may lead to a change of sign in the final result. This is likely to be a defect in the sequential program, but is well-defined in C++. It is still most-likely to be a defect in the concurrent program.
Wording
For the illustrative purpose of showing the impact of the changes to unblock P0493R4, we provide wording that gives fetch_min/fetch_max the fminimum_num/fmaximum_num semantics. It provides sounder semantics for non-floating-point experts and better performance by default. While this may alter the program outcomes while parallelizing an application, this alteration is likely to be a defect due to an assumption that either NaNs were not present in the input, or that the change -0 == +0 to -0 < +0 would not impact the current program. That being said, it introduces inconsistency with the meaning of “min” and “max” in the standard. The scalar fminimum_num/fmaximum_num C23 APIs should become available in C++26, closing the gap with sequential programs.
Therefore, we modify [atomics.ref.float] in P0493R4 as follows:
Remarks: For fetch_max and fetch_min, the maximum and minimum computation is performed as if by max and min algorithms [alg.min.max]std::fmaximum_num and std::fminimum_num [c.math.syn], respectively, with the object value and the first parameter as the arguments.
This requires updating the C standard to C23 (do you see the issue?), for which we’d need to modify [intro.scope#2]:
C++ is a general purpose programming language based on the C programming language as described in ISO/IEC 9899:20182024 Programming languages — C (hereinafter referred to as the C standard).
and [intro.refs]:
(1.3) ISO/IEC 9899:20182024, Programming languages — C
[…]
(1.10.2) The library described in ISO/IEC 9899:20182024, Clause 7, is hereinafter called the C standard library.
so that then we could then add these to [cmath.syn]:
namespace std {
constexpr floating-point-type fmaximum_num(floating-point-type x, floating-point-type y);
constexpr float fmaximum_numf(float x, float y);
constexpr long double fmaximum_numl(long double x, long double y);
constexpr floating-point-type fminimum_num(floating-point-type x, floating-point-type y);
constexpr float fminimum_numf(float x, float y);
constexpr long double fminimum_numl(long double x, long double y);
}
which would only be possible if the C23 standard was already published, which it isn’t.
To be able to merge this earlier into the C++26 working draft, then the alternative is to instead modify [atomics.ref.float] in P0493R4 to include the fminimum_num/fmaximum_num wording from the C23 draft:
Remarks: For fetch_max and fetch_min, the maximum and minimum computation is performed as if by max and min algorithms [alg.min.max], respectively, with the object value and the first parameter as the arguments.is performed by determining the maximum and minimum value of their numeric arguments. They determine the number if one argument is a number and the other is a NaN. For these functions, +0 is considered greater than −0.
To unblock the merging of P0493R4 into the working draft, the only requirement is picking the default semantics of fetch_min/fetch_max. Therefore, providing comparators and overloads for the different semantics, is left to a future paper (or future revision of this paper is that is deemed to be required).
References
- P0493R4 Atomic maximum/minimum.
- The Removal/Demotion of MinNum and MaxNum Operations from IEEE 754™-2018.
- Min-max functions Proposal for TS 18661 update WG14 N2273.
- ISO/IEC 9899:2024 C23 standard.
- ANSI/IEEE Std 754-2008.
- ANSI/IEEE Std 754-2019.
Atomic floating-point min/max
Document number: P3008R0.
Date: 2023-10-13.
Authors: Gonzalo Brito Gadeschi, David Sankel <dsankel@adobe.com>.
Reply to: gonzalob at nvidia.com .
Audience: SG1, LEWG.
Table of Contents
Introduction
P0493R4 Atomic minimum/maximum proposes the addition of
atomic<T>::fetch_minandatomic<T>::::fetch_maxoperations, which atomically performstd::minandstd::maxcomputations.The Varna '23 plenary rejected these semantics for
atomic<floating-point>types due to safety concerns. These semantics deviate from the current standard practice, as defined by IEEE 754-2019 recommendations and the capabilities of available hardware.This paper aims to empower the committee to ship these APIs in the C++ 26 timeframe. It reviews the semantics proposed in P0493R4 and standard practice: IEEE 754-2008, IEEE 754-2019, and available hardware support. It then explores the design space and evaluates alternative solutions.
Finally, the authors propose two coherent alternatives and concrete wording changes to align P0493R4 with some of the semantics IEEE 754-2019 recommends all vendors implement.
Survey of programming language floating-point min/max API semantics
This section provides an overview of widely used floating-point
min/maxsemantics. We will focus on how variousmin/maxsemantics handle the following “corner cases”:-0be considered less than+0(-0 < +0), or should-0and+0be treated as equivalent (-0 == +0) such that, e.g.,min(+0, -0) = +0?min(x, qNaN) = xandmin(qNaN, x) = x.min(x, qNaN) = qNaNandmin(qNaN, x) = qNaN.Explicitly and intentionally, this paper ignores:
Table 1 summarizes the semantics of the different C or C++ APIs regarding Signed Zeros and Quiet NaN handling and documents whether implementations that implement particular IEEE 754 semantics are valid implementations of the APIs.
minmax(Second[1])
fminfmaxor
-0 < +0(QoI) [2]minNummaxNumor (QoI)
minimumNumbermaximumNumberfminimumfmaximum-0 < +0minimummaximumfminimum_numfmaximum_num-0 < +0minimumNumbermaximumNumber[0] Ternary semantics:
min(x,y) = y < x? y : x,max(x,y) = x < y? y : x; both return the first argument if the arguments are equivalent.[1] In practice, the same implementation as for valid values is used, and the second argument is returned, since in the ternary expression, the conditional involving a NaN is always false.
[2] QoI: “Quality of Implementation”, i.e.,
fmindoes not require-0 < +0, but it recommends that high quality implementations implement it.C++
std::min/std::maxThe
std::minandstd::maxalgorithms have a precondition on their arguments ([alg.min.max.1]):which NaNs do not satisfy.
Rationale.
Per [structure.requirements#4] and [structure.requirements#8], which uses floating points as an example, the syntactic requirements apply to the type, but the semantic requirements only apply to the values actually passed to the algorithm.
The Cpp17LessThanComparable concept, which requires:
Which is specified in [alg.sorting#general-4]:
and is satisfied by all floating-point values with the exception of NaNs.
For valid values, implementations follow ([alg.min.max]):
which preserves equivalence between
-0and+0(godbolt):In all standard library implementations surveyed, the manifestation of the undefined behavior is to return the first argument; this is depicted in the example with “UB: qNaN” and “UB: 2”.
The behavior of these semantics are:
In concurrent programs, these semantics become even less intuitive, e.g., the sign of the result of a concurrent computation may depend on the order in which an observer sitting on top of the memory location observes the operations from different threads. If negative and positive zero are equivalent, the sign of this final result may differ across executions.
C
fmin/fmaxThe semantics of the ISO/IEC 9899:2024 (C23) standard
fmin/fmaxfunctions are compatible with implementations of IEEE 754-2008minNumandmaxNumand of IEEE 754-2019minimumNumber/maximumNumber. Thefmin/fmaxfunctions are available in C++ through the<cmath>header asstd::fmin/std::fmax.The semantics of C’s
fmin/fmax-0may be equivalent to+0(minNum/maxNum)-0 < +0allowed as QoI (minimumNumber/maximumNumberguarantee it).(collapsible) C23 fmin/fmax specification.
(collapsible) [IEEE 754-2008] minNum/maxNum specification.
That is, in the presence of a qNaN, these return the value, but signed zeros may or may not be equivalent:
IEEE 754-2019 removed
minNumandmaxNumoperations and replaced them withminimumNumber/maximumNumberandminimum/maximum. These are surveyed in the next section. The gist of the rationale for their removal from The Removal/Demotion ofMinNumandMaxNumOperations from IEEE 754-2018 is:C23
minimum/maximum/minimumNumber/maximumNumberIEEE 754-2019 removed
minNum/maxNumand recommends programming languages to provide their replacements instead:minimumNumber/maximumNumber/minimum/maximum.(collapsible) IEEE 754-2019 minimum/maximum/minimumNumber/maximumNumber specification.
(collapsible) C23 fmaximum/fminimum/fmaximum_num/fminimum_num specification.
The semantics of these functions matches for signed zero:
-0 < +0, and differs in their treatment when one argument is a qNaN:fminimumNumber/fmaximumNumber, return the Number.fminimum/fmaximum, propagate the qNaN.Impact of replacing
minwithfminimum_numTable 2 captures the impact of replacing
minwithfminimum_numis as follows:std::min/std::maxfminimum_num/fmaximum_nummin(qNaN, 2.f); // UB: qNaNmax(qNaN, 2.f); // UB: qNaNmin(+0.f, -0.f); // +0max(-0.f, +0.f); // -0fminimum_num(qNaN, 2.f); // 2fmaximum_num(qNaN, 2.f); // 2fminimum_num(+0.f, -0.f); // -0fmaximum_num(-0.f, +0.f); // +0That is, when the first input of
std::min/std::maxis a qNaN, then these switch from exhibiting undefined behavior to returning a number, and when signed zeros are involved, there is a case where the result has a different sign.Survey of hardware atomic floating-point min/max API semantics
On systems without native support for atomic floating-point min/max operations, these operations must be performed atomically, e.g., using a CAS loop, a compare-and-conditional-store loop, an LL/SC loop, or, e.g., by taking a lock, which would make the atomic not lock-free. In these systems, the memory latency overhead may outweight the cost of performing the actual arithmetic portion of the min/max operations, and extra effort may be required to ensure forward progress properties like starvation freedom, and therefore those systems are not considered here.
Table 3 surveys the publicly known Instruction Set Architectures (ISAs) with atomic floating-point min/max operations, which are all GPU ISAs:
MAX
minimumNumbermaximumNumberAOP_FMINAOP_FMAX[0]minimumNumbermaximumNumberred
minimumNumbermaximumNumberOpAtomicFMaxEXT
fmin/fmaxQoI: -0 < +0
VK_EXT_shader_atomic_float2. Hardware that implements it is listed here and here.All the architectures surveyed order
-0 < +0, treat qNaNs as missing data, and implement IEEE 754-2019minimumNumberandmaximumNumbersemantics. The SPIR-V extension requires Cfmin/fmaxsemantics, which allows-0 < +0but does not require it.The semantics vendor implement are compatible with C23’s
fminimum_num/fmaximum_num, and C’sfmin/fmax, but not with C++'sstd::min/std::maxdue to the different outcomes when signed-zeros are involved.Performance impact of
atomic<floating-point>::fetch_min/_maxsemanticsWe compare the performance impact of two different
atomic<floating-point>::fetch_maxsemantics:std::min, which lowers to a CAS-loop that performsstd::min(similar for compare-and-conditional-store), andfminimum_num, which lowers to native atomic operations,using a synthetic micro-benchmark that measures throughput in Giga Operations per Second (y-axis; logarithmic) as a function of the number of threads (x-axis; logarithmic) from 32 to 130’000 hardware threads on an NVIDIA GPU system.
Modern concurrent systems provide dozens of millions of hardware threads operating on the same shared memory.
While native in-memory atomic operations increase throughput until its theoretical peak with just a few thousand threads, the performance of compare and swap strategies decreases as the number of threads increases due to excess contention. At just a few thousand threads, the performance is already four orders of magnitude worse (~10’000x) than that of native in-memory operations. This is why vendors of highly concurrent systems provide these operations.
While most CPU ISAs lack native hardware instructions for atomic floating-point min/max, their performance impact is expected to be similar to that of atomic integer min/max. Section 9 of P0493R4 presents benchmarks comparing the performance of a CAS-based implementation against an Arm v8.1 implementation using the native atomic
ldsmaxlinstruction. The benchmark covers a range of cores, from 2 to 64. The performance improvement of the native instruction ranges between 2.75x (2 cores) to 1.7x at 64 cores. We expect this behavior to transfer to atomic floating-point min/max.We, unfortunately, do not have benchmarks for other hardware configurations at this time.
Design space
The design space can be categoratized into two groups of alternatives:
::fetch_min/_maxhave same semantics asstd::min/std::max,::fetch_min/_maxhave different semantics thanstd::min/std::max.The following table shows the subjectively most reasonable alternative of each category side-by-side, along with a summary of their advantages and disadvantages, which are analyzed in the following section.
Table 4: Comparison of best alternative of each category.
std::minsemanticsstd::fminimum_numsemanticsx.fetch_min(y);x.fetch_fminimum_num(y);x.fetch_min(y, std::less{});x.fetch_min(y);NaNs are UB &
-0 == +0.- Consistency in standard.
- Hardware acceleration by default.
min, has unportable behavior.- The convenient name has degraded performance.
- Subtle surprises when transitioning to atomics.
C++ needs to make an engineering trade-off: prioritizing consistency in the standard or prioritizing better defaults.
Alternatives that reserve
fetch_min/fetch_maxforstd::min/std::maxIn this group of alternatives, exposure of different semantics shall happen through other APIs, and we may potentially expose one or more of the following:
fetch_min/fetch_maxwithstd::min/std::maxsemantics, orfetch_fminimum/fetch_fmaximumwithfminimum/fmaximumsemantics, orfetch_fminimum_num/fetch_fmaximum_numwithfminimum_num/fmaximum_numsemantics, orfetch_min/fetch_maxAPI accepting a defaulted comparison function objectCmpthat satisfies the requirements of Compare and defaults tostd::less, potentially providing other function objects to chooseminimum/minimumNumbersemantics.The advantage of these alternatives is that they preserve the semantics of sequential code that uses
std::minwhen it is made concurrent viafetch_min.The disadvantages of these alternatives are that the
fetch_min/_maxsemantics are unintuitive for floating-point numbers and error prone, and do not benefit from any hardware acceleration available as surveyed in Table 2.Generic programmers willing to avoid these disadvantages need to opt-in to wrapping these APIs as follows:
But creating such wrappers requires developers to be aware of essentially everything discussed in this proposal until this point.
Such awareness may be enforced by not providing
fetch_min/fetch_maxAPIs for floating-point atomics at all, and instead only provide thefetch_fminimumand related APIs, requiring developers to explicitly pick the semantics, and making wrappers like the one in Listing 5 mandatory for writing generic code.Alternatives that provide
fetch_min/fetch_maxwith different semanticsThere is precendent in the C++ standard for the atomic operations semantics to deviate from the non-atomic semantics. For example,
atomic<int>::fetch_addwraps around on overflow, instead of exhibiting undefined behavior, see [atomics#ref.int-6]:In a similar spirit,
atomic<floating-point>::fetch_min/::fetch_maxoperations could be specified to be well-defined for NaNs and to respect-0 < +0.If we restricts the specification to the semantics available in the scalar floating-point functions, we have 3 different options:
fminimum/fmaximum: NaNs are propagated as errors and-0 < +0.fminimum_num/fmaximum_num:-0 < +0.fmin/fmax:-0 == +0or (QoI)-0 < +0.The semantics chosen could be complemented with a
fetch_min/fetch_maxAPI that accepts a comparison object that needs to satisfy the requirements of Compare but also allows accepting, e.g., one of a set of floating-point-specific blessed comparison-like objects provided by the standard that handle NaNs in specific ways but do not provide a strict weak ordering when NaNs are present. This enables applications to pick whether, e.g., they want to treat NaNs as missing data, or as errors, or whether they want to treat -0 as equivalent to +0, or as +0 greater than -0.For example, C++ could do some or all of:
These groups of alternatives give applications the capability to write generic code which may encounter floating-point values and then exhibits reasonable behavior and benefits from hardware acceleration, without requiring developers of being aware of most of what has been discussed in this paper.
If a developer encounters different results when porting their sequential code using
std::mintofetch_min, discovering those differences is required to notice that the developer may want to opt-in to thestd::minsemantics. This feedback loop is - for better or worse - more direct than requiring the developer to be a floating-point expert. If the differences are due to NaNs, then the original sequential program already exhibited undefined behavior, but the differences may be due to the treatment of-0 == +0in the sequential implementation, which may lead to a change of sign in the final result. This is likely to be a defect in the sequential program, but is well-defined in C++. It is still most-likely to be a defect in the concurrent program.Wording
For the illustrative purpose of showing the impact of the changes to unblock P0493R4, we provide wording that gives
fetch_min/fetch_maxthefminimum_num/fmaximum_numsemantics. It provides sounder semantics for non-floating-point experts and better performance by default. While this may alter the program outcomes while parallelizing an application, this alteration is likely to be a defect due to an assumption that either NaNs were not present in the input, or that the change-0 == +0to-0 < +0would not impact the current program. That being said, it introduces inconsistency with the meaning of “min” and “max” in the standard. The scalarfminimum_num/fmaximum_numC23 APIs should become available in C++26, closing the gap with sequential programs.Therefore, we modify [atomics.ref.float] in P0493R4 as follows:
This requires updating the C standard to C23 (do you see the issue?), for which we’d need to modify [intro.scope#2]:
and [intro.refs]:
so that then we could then add these to [cmath.syn]:
namespace std {constexpr floating-point-type fmaximum_num(floating-point-type x, floating-point-type y);
constexpr float fmaximum_numf(float x, float y);
constexpr long double fmaximum_numl(long double x, long double y);
constexpr floating-point-type fminimum_num(floating-point-type x, floating-point-type y);
constexpr float fminimum_numf(float x, float y);
constexpr long double fminimum_numl(long double x, long double y);
}which would only be possible if the C23 standard was already published, which it isn’t.
To be able to merge this earlier into the C++26 working draft, then the alternative is to instead modify [atomics.ref.float] in P0493R4 to include the
fminimum_num/fmaximum_numwording from the C23 draft:To unblock the merging of P0493R4 into the working draft, the only requirement is picking the default semantics of
fetch_min/fetch_max. Therefore, providing comparators and overloads for the different semantics, is left to a future paper (or future revision of this paper is that is deemed to be required).References